Topological Sorting – Competitive Programming Algorithms

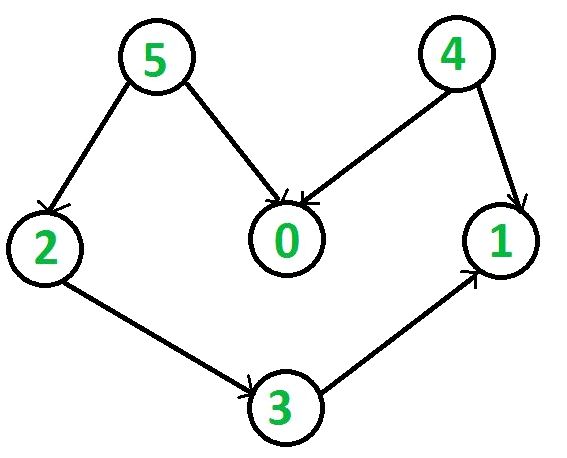
You’re given a directed graph with $n$ vertices and $m$ edges. You need to number the vertices to ensure that every edge leads in the vertex having a smaller sized number allotted to the vertex having a bigger one.

Quite simply, you need to look for a permutation from the vertices (topological order) which matches an order based on all edges from the graph.

Topological order could be non-unique (for instance, when the graph is empty or maybe there are three vertices $a$, $b$, $c$ that there are pathways from $a$ to $b$ and from $a$ to $c$ although not pathways from $b$ to $c$ or from $c$ to $b$).

Topological order may not exist whatsoever when the graph contains cycles (because there’s a contradiction: there’s a way from $a$ to $b$ and the other way around).

A typical condition in which topological sorting occurs may be the following. You will find $n$ variables with unknown values. For many variables we all know that one of these is under another. You need to check whether these constraints are contradictory, and when not, output the variables in climbing order (if several solutions are possible, output them). You can easily observe that this really is the issue to find topological order of the graph with $n$ vertices.

The Formula

To resolve this issue we’ll use depth-first search.

Let us think that the graph is acyclic, i.e. there’s an answer. Exactly what does the depth-first search do? When began from some vertex $v$, it attempts to run along all edges outgoing from $v$. It does not run across the edges that the alternative ends happen to be visited formerly, and runs along all of those other edges and starts using their ends.

Thus, when from the call $dfs(v)$ is ended, all vertices which are reachable from $v$ either directly (via one edge) or not directly happen to be visited through the search. Therefore, if during the time of exit from $dfs(v)$ we add vertex $v$ to the start of a particular list, within the finish their list will store a topological ordering of vertices.

These explanations may also be presented when it comes to duration of exit from DFS routine. Exit here we are at vertex $v$ it’s time where $dfs(v)$ finished work (the occasions could be numbered from $1$ to $n$). You can easily realize that exit duration of any vertex $v$ is definitely more than exit duration of any vertex reachable from this (ever since they were visited either prior to the call $dfs(v)$ or during it). Thus, the preferred topological ordering is sorting vertices in climbing down order of the exit occasions.

Implementation

Here’s an implementation which assumes the graph is acyclic, i.e. the preferred topological ordering exists. If required, it is simple to make sure that the graph is acyclic, as described within the article on depth-first search.

C++ implementation Show/Hide

int n // quantity of vertices
vector> adj // adjacency listing of graph
vector visited
vector ans
void dfs(int v) 
    ans.push_back(v)
void topological_sort() obvious()
    for (int i =  i < n ++i) 
    reverse(ans.begin(), ans.finish())

The primary purpose of the answer is topological_sort, which initializes DFS variables, launches DFS and receives the solution within the vector ans.