Safety Analysis for Resilient Complex Socio-Technical Systems with an Extended Functional Resonance Analysis Method

Abstract

The safety of complex Socio-Technical Systems highly depends on the non-linear interaction of variabilities between task performances in human, machines and working environments and proper management of those is essential to ensure the safety. However, the practical means to ensure the safety of those systems have not been established yet, and this is mainly due to the gap existing between the theory and the reality as well as to the lack of means for visualizing the potential risks. In this paper, we propose an extended method of FRAM: Functional Resonance Analysis Method and construct a simulator that enables to visualize the potential risks. Then, an example of interactive analysis using the simulator is presented, which enables us to visualize the degrees of resilience of an existing work procedure in operation in facing with potential variabilities. In the end, how to utilize the proposed method for the establishment of the resilient systems from the point of view of the design of operation procedures is presented.

Keywords

Functional resonance analysis method, Resilience engineering, Complex adaptive system

Introduction

Ensuring the safety of current complex systems that is called Socio-Technical Systems requires a new approach. Systems have been becoming more and more complex, forming a SoS: System of Systems for last few decades []. Socio-Technical System is the SoS such that not only technical factors but also human and organizational factors are interrelated each other. For example, operations and managements of airliners, railways and nuclear power plants are all regarded as Socio-Technical Systems. The safety of those systems should be investigated not only based upon the conventional cause-effect relationships but also upon the idea of emergence in which unexpected relationships are to be brought about as a result of interactions among various factors.

What plays an important role in the safety of Socio-Technical Systems is the interaction of system’s agents including human agents, machine agents as well as their surrounding entities. Moreover, the interaction of variabilities between task performance in human or machines and working environment is considered to have a significant effect on the safety of the system []; their interaction does make the performance as an entire Socio-Technical System variable with respect to time. Therefore, the appropriate management of such performance variability as an entire system is critical issue rather than investigating the simple malfunctions of machine or human errors for the safety of Socio-Technical Systems.

Regarding this issue, Resilience Engineering [] has received much attention these days. Resilience is defined as “the ability to manage the performance variability of the system not to get into catastrophes”, and this is achieved by the proper adaptation of agents in the system to a context where the system is operated. However, no practical means for designing and evaluating resilient systems has been established yet. This is mainly due to a gap existing between the theory and the reality as well as to the lack of means for visualizing the potential risks; the knowledge for the resilient systems has not been organized yet, and we also have no means to validate them. Thus, a first step of the solution is to establish practical means to evaluate and visualize the potential and latent risks of Socio-Technical Systems.

As for a prior work dealing with such variabilities and their interactions as mentioned above, Hollnagel proposed an idea of FRAM: Functional Resonance Analysis Method [,] that provides the guidelines for analyzing the complex dynamics emerging out of interactions among components making up the Socio-Technical Systems. Wherein, a function is defined as what has to be done to achieve a specific goal, and this methodology evaluates how the variabilities and their interactions among functions influence the progress status of functions. However, FRAM also has a limitation: FRAM is essentially a theoretic method, and there exists a gap between theory and practice.

In this paper, we show a practical way of FRAM: Fuzzy CREAM [] is integrated into FRAM, which enables FRAM’s quantitative analysis. Then, we apply a proposed method to an actual air crash accident to show how the proposed method visualizes the dynamics of variabilities among functions, and moreover, the latent risks of Socio-Technical Systems. In the end, we discuss how the proposed method can contribute to establish practical means for the design, evaluation and analysis of the resilient systems.

Safety of Socio-Technical Systems

General

The development of technology and growing complexity of society have been making artifacts more and more complex, resulting in building Socio-Technical Systems, and what the safety of them depend on has been changing. Traditionally, the safety of artifacts is considered to be ensured by eliminating the malfunction of mechanical components or human errors. However, the appearing complicated behaviors of Socio-Technical Systems are caused by the non-linear interaction between agents in the system that are becoming important factors for the safety and brittleness of artifacts. Specifically, the interaction of variabilities between task performances in human or machines under a particular working environment is considered to have a significant effect on the safety of the system [].

Figure 1 shows an overview of what should be considered for the safety of Socio-Technical Systems. Ideally, the systems are supposed to be operated in accurately executing predetermined operational procedures, while adhering the instructions or rules issued by organizations such as company or government. However, in reality, there may exist the variabilities of working environment caused by the temporal conditions such as available resources (e.g. time) or existence of simultaneous goals to be attained. Also, current high technological systems enabling automated operation often demand operators too complex procedures. To deal with these factors properly, predetermined procedures are no longer always feasible, resulting in adaptation of them to a situation that the operators are facing (e.g. the deviation from SOPs: Standard Operation Procedures). Here, it should be noted that there is a kind of trade-off in the operation; though operators are fundamentally required to execute predetermined procedures precisely, they should perform them in a more efficient way to cope with the situation. This is called ETTO: Efficiency Thoroughness Trade Off principle, and in most cases, the operation of Socio-Technical Systems cannot escape from this dilemma []. As a result of the adaptation, the variabilities of task performance in humans and/or machines are generated, and interaction of these variabilities may lead to the variability of performance as the entire Socio-Technical Systems.

Therefore, a state of Socio-Technical Systems is not bimodal: Success or Failure but multimodal: The performance is variable, and controlling such performance variability of an entire system is critical issue for the safety of Socio-Technical Systems. In other words, validating the actual work as a result of adaptation must be required for ensuring the safety of Socio-Technical systems.

Resilience engineering

There exist several definitions of Resilience, and in this paper, we define it as “the ability to manage the performance variability of the system not to get into catastrophes”. A simple illustration which represents the above definition is shown in Figure 2; though high time pressure degrades the performance or safety of the system, even in such a case proper counter measures could avoid catastrophes.

A key to establish resilient systems is how well the agents in the systems can perform in a specific context where the system is operated. However, the relations between work as imagined (e.g. the design of SOPs) and work as done (e.g. “proper counter measures” as illustrated in Figure 2) still remains unclear after all; there are no standard tactics for them.

So far, the ability/knowledge for the system’s safety has been sought for by removing or weakening the causes of adverse outcomes. That is, it was aiming at achieving a stationary state in which “there is no unacceptable risk or undesirable state never happen”. However, the resilience is a dynamic and proactive concept to realize “systems can continue to operate without falling to catastrophic state”, and there has been no means to validate the counter measures or to reproduce their effectiveness.

One approach to overcome this problem is to analyze the feasibility of SOPs: Standard Operation Procedures. In most cases, SOPs are prepared for operating mechanical systems properly. They are developed guaranteeing operators’ stagnant execution of operations. However, it is not always the case, and the issue is often discussed especially in the operation of highly automated systems.

Automation is originally believed to be introduced to reduce the workload of humans and improve the accuracy of task performance. However, it is also pointed that the introducing automation brings about changes to what the operators must do (e.g., change from direct manipulation to the supervision of instruments or task management), and influence other tasks of humans []. This could make SOPs too complex to execute precisely and cause dilemma based on the ETTO principle, resulting in deviations from them.

Especially in an aviational field, highly advanced technological automation was introduced to the cockpit earlier than any other fields, and a number of experiences concerned with this issue have been accumulated. For example, Degani, et al. investigated the design of flight-deck procedures that are involved in three major U.S. airlines []. In the study, they did several activities such as interviewing those who work for airline, attending procedure design meetings and jump seat observations and found several cases that the deviation from SOP actually occurred for the sake of efficient or comfortable flight. Then, they concluded that there is nothing such as an optimal set of neither procedures nor “royal road” to procedure development. In other words, even in highly proceduralized system, the room for individualism remains for the execution of SOPs. Moreover, Kirlik discussed about the complexity of the procedures for using automation in aviation, and verified in experiments that most of the pilots do not use automation aids in the crowded air space because of the possible requests from ATC to change the heading and altitude, that makes pilots heavily stressed since the flight deck procedures for changing automation settings [].

From the above, it seems that the deviation from SOPs is sometimes successful (resilient) and sometimes not. Then, the first step of Resilience Engineering is to establish the practical means to evaluate and visualize such degree of safety of Socio-Technical Systems.

Many methodologies of safety analysis were proposed in the past. However, almost all of them are based on cause-effect relationships and do not take the variabilities and their interaction into account, which is the core of safety in Socio-Technical Systems. To overcome this problem, Hollnagel proposed a new safety analysis method: Functional Resonance Analysis Method (FRAM) [,].

FRAM: Functional Resonance Analysis Method

FRAM: Functional Resonance Analysis Method analyzes how the variabilities and their interactions among functions influence the performance of them. This method can investigate actual events caused by non-linear interactions of variabilities. Also, it enables to simulate behavior of system against variabilities with “If-Then Exercise”.

FRAM starts with identifying functions. Function is defined as what has to be done to achieve a specific goal such as each item in a procedure. It is defined with six aspects as shown in Table 1, which enables to represent dependencies between functions as a network. If the purpose of analysis is an investigation of some anomalous events, function can be obtained from databases concerning with those events such as accident reports. Also, if the purpose of analysis is the simulation of behavior of system against variabilities with “If-Then Exercise”, some methodologies such as HTA: Hierarchical Task Analysis [] are available.

After the functions are identified, potential couplings arise among the functions. Potential couplings are the dependencies which can exist among functions. An easy way to obtain these couplings is considering linguistic relationships between the output of one function and five aspects (Input, Precondition, Resource, Control, Time) of the other functions. For example, suppose that we have three functions: START A CAR, RELEASE FOOT BRAKE, and FASTEN SEAT BELT. The function: START A CAR is triggered by releasing the foot brake, and seatbelt must be fastened before departure. Therefore, the input of START A CAR is “Foot brake is released”, and the precondition of this function is “Seatbelt is fastened”. In other words, the output of RELEASE FOOT BRAKE and FASTEN SEAT BELT can be the input and precondition of START A CAR, respectively. At the moment, this approach is qualitative rather than quantitative, and the more systematic way to find these couplings is expected [].

Given a set of functions, there may exist a variety of procedures, with which the functions are attained. That is, some functions might be totally ordered, while some functions are partially ordered, and the order of attaining some functions may be reversible, while some or not. Sometimes, a specific function may be a means for attaining other function, or might be redundant function to be excluded according to other backup functions. These are depending upon how the functions are connected each other through which aspects. Based upon the above, we here define an abstract concept that covers all possible implementations of the given set of functions as a “procedure prototype” which is then instantiated as one of a “procedure instance” variously. A standard operation procedure as “work-as-imagined” might be one of such instances, and other procedures that emerge as “work-as-done” are other possible instances. This is shown in Figure 3. Since all the procedure instances generated as the above are not always valid to attain the give functions under a given variabilities of working conditions/contexts. Therefore, we develop a method for validating and verifying each of the procedure instances extending the original methodology of FRAM.

Once the variabilities in some functions of a specific instance are generated, they propagate and interact with the variabilities in other functions, which influence the performance of each function. Also, they could resonate in a specific context, which changes the situation significantly. FRAM can analyze and represent this, which is one of the most characteristic points of this method.

However, FRAM has fundamental difficulties: Though FRAM is expected to evaluate the safety of Socio-Technical Systems under the influence of variabilities and their interactions, the definitions of those parameters are too qualitative, which makes the systematic and objective FRAM analysis difficult.

In addition, the above problem causes another one: FRAM analysis has to be done manually because the procedure of FRAM cannot be implemented. Therefore, a number of limitations for FRAM analysis remains, and it is almost impossible to perform a proper way of FRAM.

To overcome this problem, we propose a way to evaluate the variabilities and interactions numerically. Also, we implement the proposed method and build a FRAM simulator. The detail of proposed method will be shown in the next section.

Safety-I & Safety-II

Safety-I and Safety-II are the concept to enhance safety, and the paradigm shift from Safety-I to Safety-II is suggested []. Also, Resilience Engineering is thought to be based on the idea of Safety-II, each of them is defined as following:

Safety-I: Safety is enhanced by eliminating potential hazards or what goes wrong as many as possible.

Safety-II: Safety is enhanced by focusing on and pursuing what goes right.

Safety-I is based on the following idea: Conventionally, it was thought that a state of the systems is bimodal: Function or Malfunction as shown in Figure 4. That is, sources of success and failure are completely different each other. Therefore, eliminating the source of failure such as malfunction of machines or human errors is thought to directly enhance the safety.

However, situation has been changing as the growth of complexity in mechanical systems and society: a state of systems can be multimodal in the sense that they are variable and flexible. In other words, success and failure are equivalent because they come from the same source, depending on the context as shown in Figure 5.

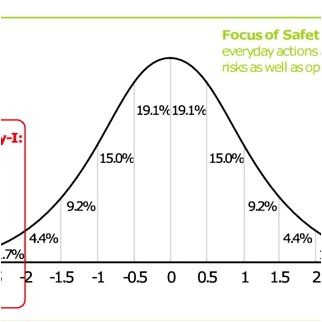
If the success and failure are equivalent, focusing on what goes wrong is no longer effective way to enhance safety. The distribution in Figure 6 represents the frequency of events with respect to the ease of perception; the event becomes acceptable as the value on the abscissa increases. As shown in Figure 6, the frequency of unacceptable events such as accidents is very low, and almost all of events are occupied with daily normal or successful events. Therefore, based on the equivalence of success and failure, not only the events such as accident but also daily normal or successful events must be focused on. Moreover, since almost all of events are occupied with latter, focusing on and pursuing what goes right has a significant effect on the enhancement of safety, which is the principle of Safety-II. Here, it should be noted that Safety-II does not neglect what goes wrong or Safety-I. Safety-II considers whole events as shown in Figure 6.

Method

Numerical evaluation of variabilities

To evaluate variabilities in a numerical way, we introduce Fuzzy CREAM, an advanced CREAM: Cognitive Reliability and Error Analysis Method []. It enables to evaluate variabilities of working environment and functions numerically, leading to establish the systematic way of FRAM.

CREAM: Cognitive Reliability and Error Analysis Method

CREAM is the second-generation form of HRA: Human Reliability Analysis, which investigates how events are going well based on the evaluation of CPCs: Common Performance Conditions. Conventionally, in first-generation HRA (e.g. THERP: Technique for Human Error Rate Prediction), human error was thought to stem from inherent deficiencies and the fact that humans naturally fail to perform tasks just the same as machines or structures can fail. However, extensive study revealed that contextual conditions under which a task is performed have a greater effect on human failure, which led to the development of the second-generation HRA. As a representative method of the 2^nd generation HRA, a methodology of ATHEANA was suggested []. In recognizing that the environment and the surrounding context may affect the human operator’s behavior, the ATHEANA methodology is to take account of what are known as Error-Forcing Contexts (EFCs), which are then combined with Performance Shaping Factors (PSFs). It can analyze the occurrence of an actual unacceptable event, and the result can show the way to improve the safety.

CREAM is an extended method of ATHEANA. In CREAM method, Hollnagel referred to the contextual conditions collectively as the CPCs: Common Performance Conditions, and defined and classified them into the nine factors: “Adequacy of organization”, “Working conditions”, “Adequacy of Man-Machine Interface”, “Availability of procedures”, “Number of simultaneous goals”, “Available time”, “Circadian rhythm”, “Adequacy of training and experience”, and “Crew collaboration quality”. Each of the CPCs contains various CPC levels and CPC effects as shown in Table 2. For example, if the CPC “Working conditions” in Table 2 is rated as “Advantageous”, it has a “Positive” effect on the situation. All CPCs are evaluated in the same way, and the number of CPCs whose effect is found to be “Negative” or “Positive” will be obtained in the analysis.

After the evaluation of all CPCs, their effects are updated according to the dependency among CPCs. Some of CPCs are interrelated each other, and their relationships are shown in Table 3. If the effect of CPC in the left column of Table 3 is “Not Significant” and more than three or four CPCs in the right column of Table 3 are “Positive”/”Negative”, the effect of CPCs in the left column of Table 3 also become “Positive”/”Negative”.

Based on the evaluation of CPCs above and the chart shown in Figure 7, Control Mode which represents how events going well are identified. Four different Control Modes are defined and the intervals of PAF: Probability of Action Failure are related to each of them as shown in Table 4. Here, note that the chart in Figure 7 has a premise that the weight of CPCs which represents how the CPC plays an important role in the target event of analysis are all equivalent.

Fuzzy CREAM

To make CREAM quantitative, several studies introduced fuzzy logic theory into the original method [,], which is generally called Fuzzy CREAM. In Fuzzy CREAM, membership functions of CPC levels whose support set is CPC score are defined. CPC score is a continuous value varying from 0 to 100, representing the status of the CPC; the higher the CPC score is, the better the CPC status is. Also, membership function represents the degree of matching between a specific CPC score and a particular CPC level, which varies from 0 to 1.00. In addition, membership functions of Control Modes whose support set is logarithm of PAF are defined. Then, linguistic fuzzy rule of CPC level and Control Mode is built. The example of the rule is following:

IF S₁ = Compatible AND S₂ = Efficient AND … AND S_m = … THEN C = Strategic

Where S_i denotes the level of the i-th CPC, m is the total number of CPCs and C represents the Control Mode (1 ≤ i ≤ m). With above items, conclusion fuzzy set of Control Mode is obtained by calculating how the antecedent matches to consequent in the If-Then rules.

Based on this fundamental idea, several studies proposed specific algorithms. For example, in the former study [], 46,656 fuzzy rules were constructed by hand and using the chart in Figure 7. Then, the conclusion fuzzy set is obtained by the min-max inference technique []. Also, in the latter study [], relative weight of CPCs are defined, and the belief degrees of each Control Modes with respect to a fuzzy rule are calculated the Bayesian network of CPCs.

There exist several algorithms for Fuzzy CREAM as shown above, and we adapt weighted CREAM model []. This is because the method takes the weight of CPCs into account, and the chart in Figure 7 is not necessary, which is not the case with other methods. weighted CREAM model consists of following four steps:

Step 1: Definition of membership function for linguistic values of CPC Levels
The first step of this method is defining membership functions, whose examples are shown in Figure 8. As for CPCs, since they have three or four CPC levels, the membership functions can be defined like Figure 8a and Figure 8b. Also, the membership functions of Control Modes can be defined like Figure 8c. In Figure 8c, the logarithm of the probability, whose base is 10, is used in the abscissa for better output: The lower limit of PAF is assumed to be 0.50 × 10^-5 according to the original CREAM (Table 4), and the logarithm of this is -5.30, i.e. the minimum value of the support set is -5.30 of Figure 8c.

Ideally, the membership functions should be designed with statistical data and/or the knowledge of experts. However, they are all regarded as simple triangular functions, shown in Figure 8, for the sake of simplicity in this paper.

Step 2: Construction of fuzzy rules
In this step, fuzzy rule is constructed systematically. Ideally, the rule should be obtained with the statistical data and/or the knowledge of experts. However, since each of nine CPCs has three or four CPC levels as shown in the example in Figure 8, tens of thousands of combinations of CPC levels are obtained as antecedents of the rule. For example, in the case of Figure 8, two levels are identified when a CPC score is evaluated and 2⁹ combinations of CPC levels are obtained as a result of the evaluation of all nine CPCs. Therefore, some systematic way to selectively define the rules as shown below is required.

$IF[\begin{array}{c}{S}_{}\end{array}1,\text{1}=\dots AND\dots AND{S}_{1,m}\text{=}\dots S_{2,\text{1}}=\dots AND\dots AND{S}_{2,m}\text{=}\dots \\ ⋮\ddots ⋮\\ S_{1,\text{1}}=\dots AND\dots AND{S}_{1,m}\text{=}\dots \\ ⋮\ddots ⋮\\ S_{n,\text{1}}=\dots AND\dots AND{S}_{n,m}\text{=}\dots \\ ]$ THEN C = C^k

Here, n is the total number of combinations of CPC levels belonging to the k-th Control Mode: C_k (1 ≤ k ≤ 4). Also, S_l,i represents the level of the i-th CPC in the l-th combination of CPC levels as the antecedent (1 ≤ l ≤ n).

To identify which combination of CPC levels belongs to which Control Mode, the index I^l is introduced (0 ≤ I^l ≤ 100). The index is defined as following:

$I^l=\sum _{}^{}i=1m{A}_i^l.w_i\text{(1)}$

Where A^l_i is called the significance of the i-th CPC level in the l-th combination in the antecedent (0 ≤ A^l_i ≤ 100).

It is defined as the value on the abscissa where its membership function reaches 1.00. For example, the significance of “Advantageous”, “Compatible”, and “Incompatible” is 0, 50, and 100, respectively in Figure 8a. Also, w_i is the normalized relative weight of the i-th CPC (0 ≤ w_i ≤ 1.00), and the normalizing process is defined as following equation:

$w_i=\frac{}{}{W}_i{\sum }_{}^{}i=1m{W}_i\text{(2)}$

Where W_i is the relative weight of the i-th CPC defined by analysts (W_i ≥ 0).

I^l is regarded as a percentage on the abscissa in Figure 8c; the value on a specific point of the abscissa: SV ^l is obtained by following equation (-5.30 ≤ SV ^l ≤ 0).

$S{V}^l\text{=-5}\text{.30}\times \frac{}{}{I}^{l}100\text{(3)}$

A certain combination of CPC levels (If-part) which belongs to a linguistic value of the Control Mode: C_k (Then-part) is identified by comparing SV ^l with the intervals listed in Table 5, which are defined by applying OR operation of fuzzy theory for Figure 8c.

Step 3: Acquisition of fuzzy conclusion
In this step, the conclusion fuzzy set of Control Mode is obtained by the calculation of µ^Ck: The degree of matching for each linguistic value of Control Modes. µ^Ck is obtained by the following equations:

${\mu }_l^{}{C}_k=\sum _{i=1}^m{\mu }_{}^{}l,i{C}_k\left(x\right).w_i\text{(4)}$

${\mu }^{}Ck\text{=}\frac{{\sum }_{}^{}}{l\text{=1}}\text{(5)}$

Where ${\mu }_{}^{}l,i{C}_k\left(x\right)$ is the value of membership function which represents the level of the i-th CPC in the l-th antecedent whose linguistic consequent is C_k, all of which vary from 0 to 1.00. Also, x is the CPC score varying from 0 to 100 evaluated during the analysis.

By using µ^Ck, the conclusion fuzzy set: µ(y) is obtained. It is defined as following:

$\mu \left(y\right)\text{=}min(max(v^{}{C}_1\left(y\right),{\mu }^{C_1}),max(v^{}{C}_2\left(y\right),{\mu }^{C2}),\dots \text{,}max(v^{}Ck\left(y\right),{\mu }^{C_k}),\dots )\text{(6)}$

Where ν^Ck(y) is the membership function of the linguistic values of the k-th Control Mode (0 ≤ ν^Ck(y) ≤ 1.00), and y equals log(PAF) varying from -5.30 to 0.

Step 4: Defuzzification
After the conclusion fuzzy set is obtained, it is transformed into a crisp value by a process called defuzzification. The crisp value is obtained by

$CV\text{=}\frac{}{}\underset{D}{\int }y.\mu \left(y\right)dy\underset{D}{\int }\mu \left(y\right)dy\text{(7)}$

Where CV is the crisp value of log(PAF) and D is the domain of integration.

Integration of Fuzzy CREAM into FRAM

To develop a systematic way of FRAM, Fuzzy CREAM is applied to each functions of FRAM, and an equation which represents dependencies among functions is introduced. That is, we realize FRAM as Fuzzy CREAM through the dependencies among functions.

First, we add two more CPCs, “Availability of resources” and “Quality of communication” to the original nine. A series of CPCs can be defined depending on the case and they were added when FRAM was proposed for the first time [].

Then, the dependencies among CPCs in Table 3 are formulated as following:

$x_i^{}{t}^{*}\text{+1}\text{=}{x}_i^{t^{*}}\text{+}\sum _j(x_j^{}{t}^{*}-x_i^{t^{*}})\times w_j\text{(8)}$

Where $x_i^{}{t}^{*}\text{+1}$ is the updated score of the i-th CPC in the left column of Table 3, and $x_i^{}{t}^{*}$ is its original score. Also, $x_j^{}{t}^{*}$ is the score of the j-th CPCs listed in the right column of Table 3, and w_j is the normalized weight of the CPC.

In addition, the dependencies among functions or how variability in a upstream function propagates to downstream functions is formulated as following:

$x_{}^{}i,downt\text{+1}\text{=}\frac{PA{F}_{}^{}}{up}\times x_{i,down}^t\text{(9)}$

Where $x_{}^{}i,downt\text{+1}$ and $x_{}^{}i,downt$ are the updated and original scores of the i-th CPC in the downstream function, respectively. Also, $PA{F}_{}^{}upt$ and $PA{F}_{}^{}upt\text{+1}$ respectively refer to the PAF value of a certain upstream function before and after the PAF value has been changed by the Fuzzy CREAM process. Eq. 9 represents that some specific CPC scores in the downstream functions decreases if the PAF in an upstream function increases, and vice versa.

Figure 9 illustrates how the calculation of Eq. 8 and Eq. 9 goes on. After the CPC scores in an upstream function is changed by the propagation of variabilities from other functions or manually, the CPC scores are updated according to Eq. 8. Here, the change of CPC scores represents variability in each factors of working environment, and we regard “Context” as a specific condition emerging from the synthesis of such variabilities in this method. Then, based on the CPC scores, Fuzzy CREAM process updates the PAF in an upstream function. The change of PAF in the function is regarded as a variability of the function, and it propagates to the downstream functions according to Eq. 9; the variabilities going through a certain aspect of the downstream function change the specific CPC scores in the function. This process is repeated recursively, and the variability in the downstream function propagates to further downstream functions.

The entire flow of proposed method is shown in Figure 10. After the initial setting is finished, potential couplings between functions are instantiated. In this method, the potential couplings are instantiated systematically by eliminating arbitrary s couplings out of T which is the total number of potential couplings. Therefore, the number of instances generated in this method is obtained by following equation:

$N=\sum _{}^{}s=0TTCs=2^T\text{(10)}$

Where N is the total number of instances generated in this method. Then, once some CPC scores in the functions are changed manually as a trigger of the simulation, the process shown in Figure 9 is repeated recursively. This process enables to simulate how the variabilities of working environment influence the performance variability of functions, and their propagation changes the performance of other functions. After the process is finished, the obtained result can be the initial state of next simulation. That is, it is possible to change the CPC scores of the result and simulate again, enabling the interactive analysis. Note that the process continues automatically after the CPC scores are changed manually at the beginning of the simulation. In other words, what should be done manually are initial setting and changing the CPC scores as a trigger of the process, and there is no room for intervention after that.

The proposed method enables the investigation of actual events such as accidents and the simulation of system’s behavior against variabilities. Moreover, the latter simulation makes it possible to evaluate the feasibility of SOPs which can contribute to the design of procedures.

Case Study with Proposed Method

The proposed method shown in the previous section is implemented, having built the simulator of FRAM. In this section, we demonstrate what the simulator can do with an analysis on an actual air crash accident that occurred near Cali Airport, Colombia in 1995. This was the first fatal accident of the high-tech B757 aircraft in its 13 years of exemplary service at that time.

An overview of the accident

American Airline flight 965 was about to land at the airport close to Cali, Colombia. The flight was already two hours behind schedule due to a departure delay at Miami, and it was dark outside.

During the approach, the ATC: Air Traffic Controller proposed a runway change for landing to the flight crew, who accepted it. At first, they were supposed to fly over the airport to south and then turn towards north for final approach. However, since the weather was fine, and ATC assumed it possible to make straight in, ATC proposed the course change to the flight 965. Also, some factors such as two hours delay made the crews of the flight 965 accept the proposal.

However, after the proposal was accepted, the crews of flight 965 became busy in responding to a new flight plan. Shortening the approach course generated a number of tasks that are to be performed in a very short available time (i.e., under an extremely high time pressure). They had some troubles with identifying a new approach course and got lost.

When a crewmember of American Airlines Flight 965 changed an approach course to an airport in order to recover from a delay in the schedule, he entered only “R” instead of “ROZO” in the FMC: Flight Management Computer. The FMC interpreted it as an input cord of “ROMEO” of Bogota, Columbia beginning with “R” in the same way. The crew entrusted the computer to make a course change without noticing the mistake. The airplane swerved off the original course and crashed into mountainous terrain near Cali, Columbia.

Initial setting for analysis

One of the most critical points of this accident is that the crew of flight 965 entered the wrong course into FMC. Also, although runway change is basically regarded as a normal event in daily operation, it seems to have caused the fatal error of the crews in this case. Therefore, we focus on what took place until they entered the wrong course to the FMC in this analysis. Based on this, the parameters required for analysis are defined as following.

Setting the basic items of functions

First, functions of FRAM must be identified for the analysis. They are what primary has to be done during the sequence of the accident, and we identified five functions as shown in Table 6 in this analysis. Note that the identification number of each function in Table 6 have nothing to do with the order of execution. The order or dependencies between functions are determined for the first time when the potential couplings are instantiated, and an instance is obtained.

The potential couplings between functions are identified as shown in Figure 11. They are instantiated before the calculation process starts, then they generate various instances.

Then, the relative weight of CPC in each function is defined as shown in Table 7. It represents how the CPC plays an important role for the execution of belonging function, and they were defined with following procedure in this analysis:

1. Identify CPCs which have significant effects on the performance of a specific function.

2. Let the relative weight of those CPCs: Wi in Eq. 2 be 100.

3. Evaluate the relative weight of other CPCs based on the above evaluation.

It should be noted that these values are normalized automatically with Eq. 2 in the implemented process of proposed method.

Setting the scenario

The variabilities occurred during the process of accident is realized by manually changing the CPC scores. We identified five major variabilities based on the prior investigation [], and their details are following:

Initial state: Everything was supposed to be going well. Therefore, all CPC scores of all functions is set 100 at the beginning of the accident sequence.

Variability 1: There was continuous discrepancy of communication after the flight 965 entered the control area of the airport. This reduced the score of “Crew collaboration quality” in 1. COMMUNICATION WITH ATC to 20.

Variability 2: The prior investigation [] pointed out that the runway change was accepted without sufficient review of the flight plan. This reduced the score of “Crew collaboration Quality” in 5. REVIEW OF FLIGHT PLAN FOR RWY CHANGE to 0.

Variability 3: After the acceptance of the proposal, one of the crews became busy in manual operation for descending. This reduced the score of “Available time” and “Number of simultaneous goals” in 4. DESCENDING FOR NEW APPROACH COURSE to 0.

Variability 4: The crews of flight 965 had to identify a new approach course under high time pressure. This reduced the score of “Available time” and “Number of simultaneous goals” in 3. IDENTIFYING APPROACH COURSE to 0.

Variability 5: The prior investigation [] pointed out that the letter “R” which is the initial letter of next waypoint was input without cross-checking. Also, the letter “R” was programmed as a completely different place from their destination at that time. Then, the score of “Adequacy of MMI” and “Crew collaboration quality” in 2. INPUT AND EXECUTE THE ROUTE TO FMC is set to 0.

These variabilities are imposed on all instances generated from potential couplings shown in Figure 11.

Results

As a result of simulation, the changes of PAF in functions with respect to the variabilities defined above were obtained for all generated instances. However, since the instances were generated systematically, some of them are not reasonable to execute as a procedure, and considering all of these instances is irrational. Therefore, we especially focus on two instances: The one is considered to represent the procedure executed during the sequence of accident. The other is picked up by analyst because it showed a quite different result from the former one even though the structure of those instances is so alike each other. This result implies that the safety of Socio-Technical System has something to do with the design of operation procedures.

The former instance is shown in Figure 12. The PAF or log(PAF) in each functions of this instance changed due to the variability 1 through 5, and the result is shown in Table 8; Table 8 shows the transition of log(PAF) in each function with respect to those variabilities. Also, this transition is shown graphically in Figure 13; the numbers on abscissa correspond to that of Variability 1 through 5. According to Table 8 and Figure 13, the log(PAF) of all functions increased due to Variability 1, which means the situation became dangerous. Then, the log(PAF) in almost all of functions remained constant under the influence of Variability 2 through 5. However, the log(PAF) of “Function 2” which represents 2. INPUT AND EXECUTE THE ROUTE TO FMC increased again due to Variability 5. The log(PAF) of “Function 2” reaches -0.70, which is much higher than that in other functions. Moreover, this value indicates that the Control Mode of this function is “Scrambled” which the most dangerous state is according to Table 5.

The latter instance is shown in Figure 14. The change of log(PAF) in each functions of this instance are shown in Table 9, and it is graphically shown in Figure 15 as well as Figure 13. Comparing the instances in Figure 15 to Figure 13, their behavior were quite different from each other. Especially, according to Figure 15, the log(PAF) in “Function 2” was -1.62, lower than that in Figure 13 after the Variability 5 was imposed on this instance. Also, the log(PAF) in “Function 4” representing 4. DESCENDING FOR NEW APPROACH COURSE started decreasing after Variability 3, and it reached -2.91 at the end of this simulation. The value indicates that the Control Mode of this function is “Tactical” according to Table 5. Therefore, this instance is “safer” than that in Figure 12, so to speak.

Discussion of the result of analysis

According to the result, the behavior in each instance against the same variabilities was quite different from each other, depending on the structure of them. Compared to the instance in Figure 12, the output of 5. REVIEW OF FLIGHT PLAN FOR RWY CHANGE in Figure 14 has only one connection with the other function, and this makes the difference between actual procedures represented by Figure 12 and Figure 14; the order to execute functions in Figure 14 is more explicit than that in Figure 12, whose order is 5. REVIEW OF FLIGHT PLAN FOR RWY CHANGE, 3. IDENTIFYING APPROACH COURSE, 2. INPUT AND EXECUTE THE ROUTE TO FMC, and 4. DESCENDING FOR NEW APPROACH COURSE. The result suggests that the explicit order to execute functions play an important role to make the procedure feasible in a context of this accident. In other words, the safety of Socio-Technical System could vary depending on the design of operation procedures, and catastrophes could be avoided with the proper design of procedures in adversities. It should be noted that Variability 1 through Variability 5, which are manual operations to change CPC scores, subsequently cause the resonance among CPCs, variabilities in the function, i.e. change of PAF, and the resonance among functions automatically; the dependencies among CPCs or functions, which cannot be controlled arbitrary, play a significant role in this simulation, and the result shown above cannot be obtained without such dependencies. Also, such result is peculiar to the proposed method and cannot be obtained with other safety analysis methods.

Another approach to analyzing Socio-Technical Systems has been provided in the field of social science, called activity theory. This theory originated from the psychology studied by L. Vygotsky, et al. and was developed by Y. Engeström []. In this theory, activities are understood to have a mutually linked structure, in which the three factors (communities, rules, and division of labor) are added in addition to human being, object, and mediating tools, to trace the alternation and development of activities as “a succession of contradictions” generated in this structure and among multiple activities.

The previous safety analyses have focused on unsafe acts such as human errors and/or breach of rules by frontline workers. These unsafe acts directly affect the system safety and are characterized by that the negative impacts of such acts become conspicuous relatively quickly (active failure).

On the contrary, there are latent factors, of which impacts do not become apparent quickly and lay hidden without bringing any harm, but afterward can destroy the system defense by interacting with the local environment (latent condition). People who work within a complex system commit unsafe acts, such as errors or breach of rules, by some reasons that cannot be explained with the psychology studying an individual. Such reasons continue to be hidden within organizations and never become apparent unless facing abnormal conditions resulted from the unsafe acts or others. Such latent conditions do not lay behind statically but change with time by interacting each other below the surface. The processes of such changes may lead to changes in front-line works, as well as to accidents in the worst scenario. For instance, empirical evidences of the criticality accident occurred at the nuclear fuel conversion facility of JCO (1999) are reported []. This accident was caused by the intentional transformation of work procedures by onsite workers. This transformation was driven by the various contradictions, i.e., misfits between components of the activity system, might arise out of and propagate throughout their activities, then induce some sorts of changes in the procedures for the better or for the worse.

Such procedure transformation is dealt with as adaptation of procedures in this work, and our work can contribute to visualizing the process of its changing with latent contradictions, thus contribute to the in-depth analysis of organizational accidents.

Discussion for Future Work

Design of operation procedures

In future work, we consider the design of operation procedures as an effective way to practice Resilience Engineering with our proposed method. As already described, what is important in resilient systems is adaptations of agents to a specific context where the system is operated. Also, the safety of the systems could vary depending on the design of procedures in a specific context, and the result of simulation in the previous section suggested that. Therefore, one goal to make the systems resilient is to find out proper actual works for safe operations in specific contexts, and we call it, in this context, “design of operation procedures”.

The process is to modify predetermined procedures with elaborate validation as shown in Figure 16. To validate the design of procedure, we use the simulator of FRAM proposed in this paper as a tool of stress test of procedures in a specific context. The simulator can evaluate the feasibility of procedures in a specific context which can be represented by the score of CPCs, and this stress test can contribute to finding out proper actual works. Here, it should be noted that this process is intended to evaluate the validity of adaptation shown in Figure 1.

Safety analysis based on Safety-II

To consider the Resilience Engineering, not only why things go wrong but also why things go right must be taken into account. Resilience can be regarded as making systems go right under the influence of variabilities of working environment. Therefore, only considering why things go wrong such as accident analysis is insufficient. Considering this, we also have to focus on good practices when we carry out case studies. Unfortunately, the lessons learned so far have mainly focused on risks and been deduced from an analysis of failures that led to the accident. However, in addition to those, we should learn from good practices, in which the original operational procedure was violated by the execution of some non-regulated actions allowing any “further catastrophe” to be avoided. For instance, the accident known as the “Miracle on the Hudson” in 2009 was one of these cases []. Inspite of the existence of potential lessons to be learned, there has been almost no analysis, assessment nor lessons gleaned with respect to such good practices.

Our proposed method of FRAM could contribute to this purpose; the FRAM can evaluate validity of actual works and give us clues to figure out why they are working well in a particular context. This contributes to extending a particular success to a more generalized lesson that are valid even in a changing environment, and derives new lessons to improve the capability to handle “unforeseen contingencies”. The knowledge obtained from this visualization could especially contribute to adaptation or modification of procedures in the design of operation procedures. Finally, we accumulate the result of those simulations which contain the authorized knowledge about actual works and generalize it for the proper design of operational procedures. This consequently contribute to the cross-industrial enhancement of safety.

Conclusion

Ensuring the safety of Socio-Technical Systems requires a new approach. What plays an important role in the safety of Socio-Technical Systems is the interaction of variabilities between task performance in human or machines and working environment, and the proper management of them is essential for ensuring the safety. Concerned with this issue, Resilience Engineering has been attracting attention these days. However, there are no standard tactics to practice Resilience Engineering due to the gap between theory and practice.

To overcome this problem, we proposed a method to visualize the safety of Socio-Technical System as a first step of Resilience Engineering. For the purpose of it, safety analysis method FRAM was extended by integrating Fuzzy CREAM into it.

Then, the proposed method was applied to the actual air crash accident. The result of analysis showed the safety of the system can vary depending on the design of procedures, and it might be able to avoid catastrophes even if the system gets into adversities.

In future work, we explore how to make Socio Technical Systems resilient by considering the proper design of operation procedures. The proposed method is used as a tool of stress test of operation procedures, and the knowledge for the proper design of them is accumulated. They are finally generalized, contributing to the cross-industrial enhancement of safety.